현대 포트폴리오 이론 (Modern Portfolio Theory 이하 MPT)
포트폴리오 이론은 해리 마코위츠에 의해 체계화된 이론으로 자산을 분산 투자하여 포트폴리오를 만들게 되면 분산투자 전보다 위험을 감소시킬 수 있다는 이론이다. - Wikipedia
지배원리와 효율적투자선
'계란을 한 바구니에 담지 마라'라는 말을 들어보셨을 겁니다. 한 바구니에 담긴 계란은 떨어지게 되면 다 같이 떨어지기 때문에 여러 바구니에 나눠 담아 리스크를 분산하라는 의미로 쓰입니다. 포트폴리오 이론과 함께 지배원리라는 것을 알아야 합니다.
지배원리는 시장에 존재하는 무수히 많은 자산을 조합하면, 수많은 포트폴리오를 만들 수 있고 이러한 포트폴리오들 중에서 동일한 위험을 지녔으나 기대수익이 높거나, 동일한 기대수익을 가져다 주지만 위험이 낮은 포트폴리오는 그렇지 않은 포트폴리오를 지배한다. 이러한 지배원리를 통해 서로 지배할 수 없는 포트폴리오들의 조합을 효율적 투자선이라고 한다. -Wikipedia
간단히 말해 투자하고 있는 종목들의 리스크를 줄이기 위해선 여러 종목을 나눠서 투자하는 것이 더 안전하고,
만약 같은 수익을 가져다주는 두 포트폴리오가 있으면 위험도가 더 낮은 포트폴리오를 선호하고, 같은 위험도를 가진 두 포트폴리오가 있으면 수익률이 더 높은 포트폴리오를 선호하기 때문에 효율적 투자선이라는 것이 등장했습니다.
효율적 투자선의 X축은 Standard Deviation(표준 편차) 즉 위험도, 변동성을 의미합니다. Y축은 수익률을 의미하죠.
예를 들어 지난 1년간 제가 A 주식에 50% 투자하고 B 주식에 50% 투자하고 있다고 가정합시다.
A주식의 연간 수익률 : 10% 연간 표준편차 : 10%
B주식의 연간 수익률 : 20% 연간 표준편차 : 20%
현재 제 포트폴리오는 그래프상으로 다음 지점에 있을 것입니다.
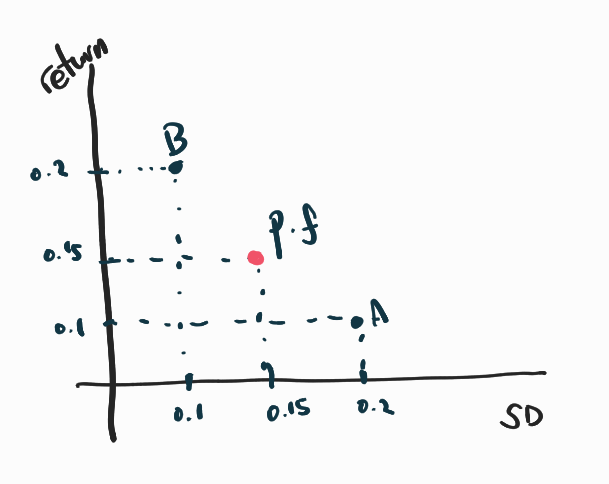
만약 A 주식에 40%, B 주식에 60%를 투자했다고 한다면, 점은 X축이 0.14, Y축이 0.16에 찍혔을 것입니다. 이처럼 0~100% 까지 비중을 조절하면서 모든 포트폴리오를 점을 찍어보면(공매도가 가능하다고 가정하면 - %까지 가능합니다) 다음과 같이 나올 것입니다.
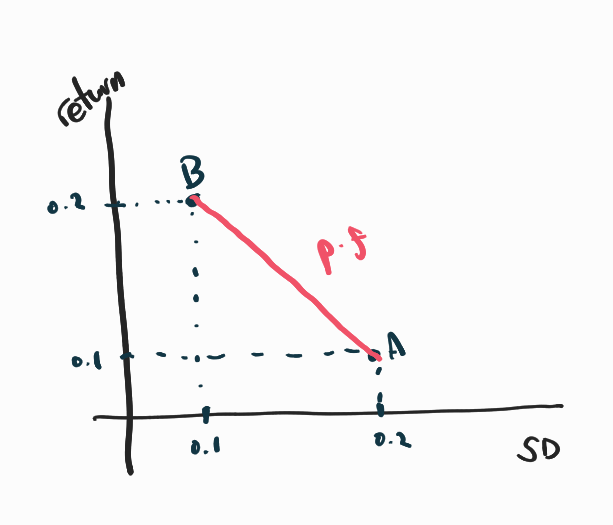
이 경우는 A주식과 B주식의 상관계수가 1이기 때문에 직선으로 그려졌지만, 자산들의 상관계수는 서로가 1인 경우가 거의 없기 때문에 대부분 곡선으로 그려집니다. 또한 이 경우는 두 종목만을 했기 때문에 비교적 간단했지만 그 수가 많아진다면 다음과 같은 그래프가 그려질 것입니다.

A, B, C, D, E에 투자할 때 그림처럼 무수히 많은 점(포트폴리오)이 찍힙니다.
앞서 지배원리는 같은 위험도를 가진 포트폴리오라면 더 높은 수익률을 내는 포트폴리오가 지배하고, 같은 수익률을 가진 포트폴리오라면 더 낮은 위험도를 가진 포트폴리오를 지배하는 것이라고 했습니다. 그렇다면 위의 그림처럼 무수히 많은 점이 찍힐 때 이 지배원리에 입각한 효율적 투자선은 어떻게 그려질까요?

분산(위험도)을 최소화하는 공식을 통해 수익률을 높여가며 표준편차가 최소인 지점을 찍어 이으면 위 그림처럼 곡선이 생깁니다. GMV는 Global Minimum Variance 포트폴리오로 표준편차가 가장 작은 포트폴리오입니다. 즉, 가장 안전한 포트폴리오라는 것이죠.
GMV 점을 구하는 방법은 다음과 같습니다.
$ min \sigma = min \ w^T\Sigma w $
이 외에서 Max Sharpe Portfolio, Risk parity Portfolio 가 있습니다만 추후 주제로 다룰 생각입니다.
'금융 및 데이터' 카테고리의 다른 글
| [Python] FinanceDataReader 데이터 Mysql DB에 적재하기 (0) | 2023.05.25 |
|---|---|
| [R] 데이터 분석 코딩 (0) | 2021.12.14 |
| [Python] 뉴스 감성지수 분류 모델 (6) | 2021.06.17 |
| Swap curve & Curve fitting (0) | 2021.06.14 |
| [Python] Random Forest 모델 기반 변수 중요도 산출하기 (0) | 2021.06.13 |


