
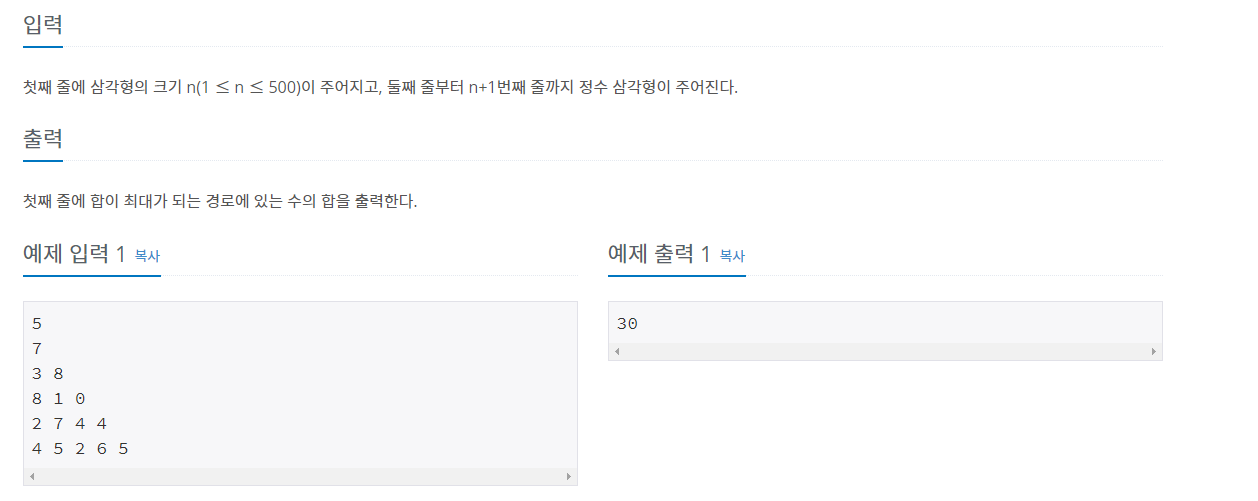
동적계획법 문제임에 따라 점화식을 구하고 메모이제이션을 어떻게 할지 먼저 구상해야 한다. 입출력에는 BufferedReader 와 System.out.println을 사용하였다.
1. 메모이제이션(Memoization)
우선 정수 삼각형을 이루고 있는 값들을 cost(비용) 이라 하면, 이 cost는 2차원 배열이 된다. 또한 최대 누적값을 저장하는 2차원 배열 DP[][] 를 만들어 i행 j열의 요소까지의 최대값을 저장하여 중복되는 계산과정을 줄일 수 있다.
예를 들어,
2
1 3
1 2 0
인 2차원 배열이 입력값으로 주어졌을 때, cost는
[2][0][0]
[1][3][0]
[1][2][0]
이 되고 DP배열은 로직을 다 돌고나면 다음과 같은 배열이 될 것이다.
[2][-1][-1]
[3][5][-1]
[4][7][5]
여기서 -1은 DP배열을 선언할 때 초기값을 -1로 설정해주었기 때문인데 이는 주어지는 해당 칸의 방문여부 즉, 계산을 거친 칸인지 여부를 확인하기 위함인데, 초기값을 0으로 설정해두는 경우가 대부분이지만 이 경우엔 주어지는 입력값 중 0이 포함되기 때문에 0으로 초기화를 하면 해당 칸의 계산 여부를 확인할 수 없게 된다.
이와 같이 DP배열이 계산되고 나면 마지막 행의 요소 중 최대값을 출력하면 되는 문제이다.
2. 점화식
이 문제는 첫 번째 행부터 각 요소마다 오른쪽 혹은 왼쪽으로 내려가면서 그 합을 누적하여 그 합을 최대로 만드는 경로를 찾아가는 문제이다. 아래층에 있는 수는 현재 있는 층의 대각선 아래로 밖에 선택할 수 없기 때문에 이를 해결하기 위해 세 가지의 경우로 나눌 수 있다.
*i=row
1. DP[i]행의 첫 번째 요소는 이전 행의 첫번째 요소만 선택할 수 있다.
DP[i][0] = DP[i-1][0] + cost[i][0]이 된다.
2. DP[i]행의 마지막 요소는 이전 행의 마지막 요소만 선택할 수 있다.
3. DP[i]행의 나머지 요소는 이전 행의 같은 열 요소와 1을 뺀 요소중 최대값을 선택할 수 있다.
public static int triangle(int N,int M){
if(DP[N][M]==-1) {
if(M==0) {
DP[N][M] = triangle(N-1,M) + cost[N][M];
}else if(M==N) {
DP[N][M] = triangle(N-1,M-1) + cost[N][M];
}else {
DP[N][M] = Math.max(triangle(N-1,M-1),triangle(N-1,M)) + cost[N][M];
}
} return DP[N][M];
}
DP배열을 -1로 초기화하였기 때문에 -1인지 아닌지에 따라 계산여부를 확인할 수 있다. 앞서 말했듯 몇 M(열)인지에 따라 점화식이 조금씩 차이가 있다.
전체코드는 다음과 같다.
package Baekjoon;
import java.io.*;
import java.util.*;
public class Main {
public static int[][] DP;
public static int[][] cost;
public static int MAX = Integer.MIN_VALUE;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
DP= new int[N][N];
cost = new int[N][N];
StringTokenizer st;
//DP 배열 -1로 초기화
for (int i=0;i<N;i++) for(int j=0; j<N;j++) DP[i][j] = -1;
//cost 배열 값 할당
for (int i=0; i<N;i++) {
st = new StringTokenizer(br.readLine());
for (int j=0;j<i+1;j++) {
cost[i][j] = Integer.parseInt(st.nextToken());
}
}
//DP 첫 번째 값에 cost배열 첫 번째 값 할당
DP[0][0] = cost[0][0];
//DP 배열 마지막 행을 반복문을 돌며 최대값을 MAX에 저장
for(int i=0; i<N; i++) {
MAX = Math.max(MAX, triangle(N-1,i));
}
System.out.println(MAX);
}
public static int triangle(int N,int M){
if(DP[N][M]==-1) {
if(M==0) {
DP[N][M] = triangle(N-1,M) + cost[N][M];
}else if(M==N) {
DP[N][M] = triangle(N-1,M-1) + cost[N][M];
}else {
DP[N][M] = Math.max(triangle(N-1,M-1),triangle(N-1,M)) + cost[N][M];
}
} return DP[N][M];
}
}

'알고리즘 스터디' 카테고리의 다른 글
| [JAVA] BOJ 1463 1로 만들기 (0) | 2021.06.29 |
|---|---|
| [JAVA] BOJ 2579 계단 오르기 (0) | 2021.06.29 |
| [JAVA] BOJ 1003번 피보나치 함수 (0) | 2021.06.26 |
| [JAVA] BOJ 9461 파도반 수열 (0) | 2021.06.26 |
| 생활코딩 - 자바 강의를 듣고 (1) | 2021.06.21 |



